Regular Expression 从理论到实现 - IV

Created on: 2022-10-1039 min read

前言

本篇文章是 Regular Expression 从理论到实践系列的第四篇文章。

在这个系列里，我将尝试从理论出发，阐述 Regular expression 作为软件开发人员不可或缺的工具背后所蕴含的计算机科学的重要理论，以及如何将这些理论付诸实践（用代码实现）。

或许对大多数开发者来说，掌握一门称手的工具更为重要。但是我希望读者们读完本系列文章之后，也能意识到理论的重要之处。

如果你还没有阅读本系列的第一篇文章，请先移步至:

Regular Expression 从理论到实践系列 - I
Regular Expression 从理论到实践系列 - II
以及 Regular Expression 从理论到实践系列 - III，否则你将无法很好地吸收和理解本篇文章。

回顾

上篇文章展示了 NFA 和 DFA 的等价性 (equivalence)，并提供了一个证明思路，然后引入了一个关于 NFA 和正则语言的重要的推论。接着文章利用 NFA 对第二篇文章中提到的三个定理重新提供了新的证明思路。

正则表达式 (Regular Expression)

本系列前三篇文章的主要内容都与有限自动机有关，而与之息息相关的理论，或许也是很多人都曾听过并且熟悉的 —— 正则表达式 (Regular Expression)。

在算数运算中，我们可以利用加减乘除运算以及括号来构建一个算数表达式，例如： $(5+3)\times 10$ 。

同样的，对于语言 (languages) 而言，我们可以使用正则运算来构建用于描述语言的表达式，这样的表达式我们称之为正则表达式 (Regular Expression)，例如：

(0 \cup 1)\circ(0^*)

算数表达式的值通常是一个数值，例如上述算数表达式 $(5+3)\times 10$ 的值为 $80$ 。而正则表达式的值则是一个语言，例如上述正则表达式 $(0 \cup 1)\circ(0^*)$ 描述了一个以 0 或者 1 开头并且以任意多个 0 结尾的语言。这个例子刻意使用了一些冗余的括号，将表达式中的每个独立的部分清楚地分隔开来，后续我们可以在不改变其含义的情况下通过省略一些符号来精简正则表达式。

该正则表达式可以拆分为两部分： $(0 \cup 1)$ 和 $(0^*)$ ，这两部分通过拼接操作符 $\circ$ 进行连接。

首先，该表达式中的 $0$ 和 $1$ 是集合 $\{0\}$ 和 $\{1\}$ 的简写（因为正则运算只能作用于语言而非单个字符或者字符串，而语言则是字符串的集合）。所以 $(0 \cup 1)$ 实际上等同于 $(\{0\} \cup \{1\})$ 。我们很容易看出第一部分所描述的语言是 $\{0, 1\}$ 。

同理，第二部分 $(0^*)$ 实际上等同于 $(\{0\}^*)$ ，它的值是包含由字符 0 构成的任意长度的字符串的语言，比如 $\epsilon, 0, 00, 000, 0000$ 等等。

其次，这两部分通过正则运算 $\circ$ 进行连接，而由于 $\circ$ 是一个非常普遍的运算，因此我们通常可以省略该运算符从而写作 $(0 \cup 1)(0^*)$ 。正如算数运算一样，不同的运算符拥有不同的优先级。对于正则运算来说 $*$ 运算的优先级高于 $\circ$ 运算, 而 $\circ$ 运算的优先级高于 $\cup$ 运算，而括号的优先级则高于其他任何运算符，因此我们可以使用括号将不同的部分组合在一起而不受其他部分的干扰。

所以，上述正则表达式我们最终可以简化为 $(0 \cup 1)0^*$ 。

留给读者思考：为什么第一个括号不能省略，如果省略了，该正则表达式含义将会发生怎样的变化？

接着再让我们了解一些特殊的表达式（符号）：

如果我们有字母表 $\varSigma = \{0, 1\}$ ，我们可以利用 $\varSigma$ 来作为正则表达式 $(0 \cup 1)$ 的简写。那么对于任意字母表 $\varSigma$ ，正则表达式 $\varSigma$ 则描述了包含了这个字母表之上的所有长度为 1 的字符串的语言。

而 $\varSigma^*$ 则等同于 $(0 \cup 1)^*$ ，这个表达式则描述了包含所有由字符 0 和 1 可能构成的字符串的语言。同理，对于任意字母表 $\varSigma$ ，正则表达式 $\varSigma^*$ 则描述了包含了这个字母表之上的所有可能构成的字符串的语言。

正则表达式在计算机应用中扮演着相当重要的角色，只要是和文字处理相关的应用，通常都少不了正则表达式的身影，用户可以利用正则表达式来搜索满足特定模式的字符串。例如 Unix 中的 awk 和 grep, 编程语言 Perl, 以及现代文本编辑器 vscode, sublime text 等工具都多多少少地利用了正则表达式。

正则表达式的正式定义 (Formal Definition of a Regular Expression)

某表达式 $R$ 被认为是一个正则表达式当 $R$ 是以下其中一项:

某个属于字母表 $\varSigma$ 的字符 $a$ ( $a$ 指代的是字母表中的任意字符)
$\epsilon$
$\empty$
$(R_1 \cup R_2)$ , 其中 $R_1$ 和 $R_2$ 都是正则表达式
$(R_1 \circ R_2)$ , 其中 $R_1$ 和 $R_2$ 都是正则表达式
$(R_1^*)$ , 其中 $R_1$ 是正则表达式

在第一和第二项中，正则表达式 $a$ 和 $\epsilon$ 分别代表语言 $\{a\}$ 和 $\{\epsilon\}$ 。而第三项 $\empty$ 代表空语言（不包含任何字符串的语言）。不难看出，第四，五，六项则可以通过对前三项进行 $\cup$ ， $\circ$ 以及 $*$ 运算来获得。如此一来，通过循环的的方式便可以不断地构造更加复杂的正则表达式。

因为 $R_1$ 和 $R_2$ 比它们构造出的正则表达式 $R$ 更小，并且最终某个 $R_1$ 和 $R_2$ 都会落入前三项中且无法再进一步拆分，这样就避免了无限循环。这种类型的定义我们也称之为归纳性定义 (inductive definition)。

表达式中的括号通常是可以省略的，如果没有括号的存在，表达式的求值遵循以下顺序：先求值 $*$ 运算，再 $\circ$ 运算，接着 $\cup$ 运算。为了方便，我们还定义 $R^+$ 为 $RR^*$ 的简写，也就是说： $R^*$ 为自身集合中的字符串 0 到任意多次的拼接，其中 $\epsilon$ 也属于 $R^*$ (如果不太熟悉可以复习第二篇文章中的相关部分)。而 $R^+$ 则保证了至少有 1 次拼接。

因此，以下等式成立：

R^+ \cup \epsilon = R^*

同时，类似于第一篇文章关于字符串和语言的部分中的内容，我们定义 $R^k$ 为 $R$ 对自身拼接 $k$ 次的简写，例如： $R^3 = RRR$

最后，为了区分正则表达式和其描述的语言，我们将正则表达式 $R$ 所描述的语言写作 $L(R)$ 。

Examples: 若干个具体的例子

为了更好地理解正则表达式，让我们再来看一些具体的例子。对于下方的例子，均假设其字母表为 $\varSigma = \{0, 1\}$ :

$R = 0^*10^*$ 所含字符串只包含一个 $1$ 的语言
$R = \varSigma^*0\varSigma^*$ 所含字符串至少包含一个 $0$ 的语言
$R = (\varSigma\varSigma)^*$ 所含字符串长度为偶数的语言
$R = (\varSigma\varSigma\varSigma)^*$ 所含字符串长度为 $3$ 的倍数的语言
$R = 01 \cup 10$ , $L(R) = \{01, 10\}$
$R = (01)\empty$ , $L(R) = \empty$ , 任何语言拼接空语言仍然是空语言
$R = \empty^*$ , $L(R) = \{\epsilon\}$ , 虽然空语言不包含任何字符串，但是 $*$ 运算拼接 0 次的结果会产生空字符串 $\epsilon$

接下来让我们观察正则表达式的一些特征，使 $R$ 为任意的正则表达式，那么以下等式成立:

$R \cup \empty = R$
$R \circ \epsilon = R$
$R \cup \epsilon$ 不一定等于 $R$
$R \circ \empty$ 不一定不等于 $R$

正则表达式在编译器的设计中也非常的实用。在编程语言中，最基本的元素，我们可以称之为 token，token 可以是变量名，常量等等。我们可以通过正则表达式来表达 token，比如下面的正则表达式则表达了数值常量：

使 $D = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$ ，那么 $(+ \cup - \cup \epsilon)(D^+ \cup D^+.D^* \cup D^*.D^+)$ 则能够表达诸如: $25, 3.1415926, +7., -.01$ 等十进制（小）数。

正则表达式和有限自动机的等价性 (Equivalence with Finite Automata)

或许对于某些读者来说，正则表达式和有限自动机似乎是截然不同的东西，他们的等价性让人感到意外。然而，任何正则表达式都可以转换成有限自动机并且识别它所描述的语言。

让我们回忆一下，在第一篇和第三篇文章中我们提到过，正则语言(regular language) 是能被某个自动机所识别的语言，而正则表达式和正则语言也有着紧密的关联。

定理

$对于某个语言，当且仅当存在某个正则表达式能够描述这个语言，这个语言才是正则语言。$

这个定理也有两个方向，我们将对不同的方向进行证明，并引出对应的引理 (lemma)。

引理 1

$如果一个语言能被某个正则表达式所描述，那么该语言是正则语言。$

证明思路 (Proof idea)

假设我们有一个描述某语言的正则表达式 $R$ ，我们可以通过将其转换为 NFA。而通过第三篇文章提出的推论我们知道，如果存在某个能够识别该语言的 NFA，那么该语言是正则语言。

证明 (Proof)

现在让我们通过将正则表达式 $R$ 转换为 NFA 来证明这个引理。接下来让我们分别考虑上文中正则表达式的正式定义中的六个情况：

$R = a, a \in \varSigma$ ，则有 $L(R) = \{a\}$ ，那么下方的 NFA 可以识别 $L(R)$ :

虽然这里我们也可以使用一个 DFA 进行构造，但是使用 NFA 会让我们的证明更加简洁。我们还可以更加形式化地表达这个过程：存在 NFA $N = (\{q_1, q_2\}, \varSigma, \delta, q_1, \{q_2\})$ ，其中 $\delta(q_1, a) = \{q_2\}$ ，并且有 $\delta(r, b) = \empty$ 对于 $r \neq q_1$ 或者 $b \neq a$

$R = \epsilon$ ，则有 $L(R) = \{\epsilon\}$ ，那么下方的 NFA 可以识别 $L(R)$ :

形式化表达：存在 NFA $N = (\{q_1\}, \varSigma, \delta, q_1, \{q_1\})$ ，并且有 $\delta(r, b) = \empty$ 对于任意 $r$ 和 $b$

$R = \empty$ ，则有 $L(R) = \empty$ ，那么下方的 NFA 可以识别 $L(R)$ :

形式化表达：存在 NFA $N = (\{q_1\}, \varSigma, \delta, q_1, \empty)$ ，并且有 $\delta(r, b) = \empty$ 对于任意 $r$ 和 $b$

$R = R_1 \cup R_2$
$R = R_1 \circ R_2$
$R = R_1^*$

第 4，5，6 项我们可以利用正则语言运算的封闭性来构造对应的 NFA，也就是说我们可以针对 $R$ 构建一个 NFA，这个 NFA 将利用已知的 $R_1$ 所对应的 NFA 和已知的 $R_2$ 所对应的 NFA (或者只使用 $R_1$ ，见第 6 项)。具体的构造过程本篇文章不再赘述，读者可自行参考第三篇文章中利用 NFA 证明正则语言运算的封闭性的过程。

以上，我们就结束上述定义其中一个方向的证明，这也是相对较为简单的方向。在我们证明另外一个方向之前，让我们来观察一些具体的例子，以便于更好地理解，如何使用上述的构建流程来将正则表达式转换为 NFA。

我们以正则表达式 $(ab \cup a)^*$ 为例，来展示如何将其转换为 NFA，我们将一步一步地从最小的单元开始构建，然后将其逐渐合并：

$ab$

$ab \cup a$

$(ab \cup a)^*$

至此，我们就完成了整个 NFA 的构建。注意，这种构建方式虽然非常标准且不会出错，但是也容易产生一些冗余的状态和状态转移。

留个读者思考：对于上述正则表达式 $(ab \cup a)^*$ ，只需要最少两个状态的 NFA 即可描述出来，你能想出来吗？

引理 2

$如果一个语言是正则语言，那么它能够被某个正则表达式所描述。$

证明思路 (Proof idea)

我们需要展示：如果一个语言 $A$ 是正则语言，那么我们可以找到某个正则表达式 $R$ 来描述这个语言。而因为 $A$ 是正则语言，那么它就能被某个 DFA 所识别 (正则语言的定义)。接下来，我们将介绍一个方法，通过这个方法，我们可以逐步地将 DFA 转换成等价的正则表达式。

接下来我们将通过两个步骤来进行证明，我们首先将 DFA 转换为一种新的有限自动机 —— GNFA (generalized nondeterministic finite automaton)。然后我们再将 GNFA 转换成正则表达式。

GNFA

GNFA 也是 NFA，只不过它的状态转移箭头上的标签不是字符（或者 $\epsilon$ ）而是正则表达式。读者可以这样想象 GNFA 的计算过程：GNFA 一次读取若干个字符，这若干个字符如果能够匹配接下来任意状态转移上标记的正则表达式，那么就可以进入下一个状态。如果计算过程最终可以使得 GNFA 进入接受状态，那么 GNFA 则接受该输入字符串。一个 GNFA 的例子如下图所示：

为了方便起见，我们要求 GNFA 总处于某种形式并满足以下条件：

起始状态有分别指向其他所有状态的箭头，但其他所有状态没有指向起始状态的箭头。
只拥有一个接受状态，并且该接受状态有分别来自其他所有状态的箭头，但没有任何指向其他任何状态的箭头。
除了起始状态和接受状态之外，其他的所有状态都有分别指向该状态本身的箭头以及分别指向其他所有状态的箭头。

DFA -> GNFA

首先我们需要增加一个新的起始状态和一个新的接受状态。

然后从新的起始状态起，我们为其添加指向其他所有状态的箭头，并设置这些箭头上的默认标签为 $\empty$ ，除非是从新的起始状态指向旧的起始状态，这种情况我们使用 $\epsilon$ 作为标签。

接着我们为所有的状态添加指向新的接受状态的箭头，并设置这些箭头上的标签为 $\empty$ ，除非是旧的接受状态指向新的接受状态，这种情况我们也使用 $\epsilon$ 作为标签。

最后，对于除了新的起始状态和接受状态外的其他状态，我们只会进行两种修改：

如果两个状态之间原本没有状态转移的箭头，或者是某个状态没有指向自己的箭头，那么我们添加一个相应的箭头，并设置标签为 $\empty$
如果两个状态之间或者某个状态指向自己的箭头上的标签有多个值，或者存在多个箭头，那么我们则只保留一个箭头，并用 $\cup$ 运算将原有标签组合为一个正则表达式。

现在让我们用一个非常简单的例子来理解一个过程，假设我们有以下 DFA，假设字母表为 $\varSigma = \{0, 1\}$ :

我们通过若干个步骤来展示这个过程:

步骤 (1)

步骤 (2)

步骤 (3)

实际上，添加 $\empty$ 并不改变原来 DFA 的计算能力，因为对于构造出来的 GNFA 而言，可以存在很多不同的计算分支，而我们可以完全忽略包含 $\empty$ 的状态转移。

GNFA -> Regular Expression

在完成了 DFA 到 GNFA 的初步转换之后，如何将 GNFA 转换为一个正则表达式呢？假设当前的 GNFA 有 $k$ 个状态，而我们知道 GNFA 必定有一个起始状态以及一个接受状态，并且这两个状态不是同一个状态，所以满足 $k \ge 2$ 。

如果 $k \gt 2$ , 我们将移除一个状态并构建一个拥有 $k-1$ 个状态的等价 GNFA。这个步骤将不断地被重复，直到该 GNFA 只剩下两个状态。如果满足 $k = 2$ ，那么说明当前的 GNFA 只有一个从起始状态指向接受状态的箭头，而这个箭头上的标签就是我们寻找的正则表达式。

假设我们有一个包含 3 个状态的 DFA，那么该 DFA 转换到正则表达式的流程如下：

接下来我们将讨论如何将 GNFA 从 $k \gt 2$ 个状态转换为等价的 $k-1$ 个状态的 GNFA。这个过程的核心是找到一个除起始状态和接受状态以外的状态，然后移除该状态，并且修正 GNFA 使其等价于未移除状态前的版本并接受同一个语言。

那么我们要如何从 GNFA 中移除状态呢？假设我们要从 GNFA 中移除状态 $q_r$ ，如下图所示：

在移除了 $q_r$ 之后，我们需要通过修改其他箭头上的标签来修正 GNFA。新的标签将会补偿缺失的状态 $q_r$ 所代表的计算，从 $q_i$ 到 $q_j$ 的箭头上的正则表达式将会描述从从 $q_i$ 直接转移到 $q_j$ ，或者经过 $q_r$ 再转移到 $q_j$ 的字符串。如下图所示：

我们可以看到，在经过了一次转换之后，该 GNFA 已经减少到只剩两个状态，因此我们可以直接读取唯一的箭头上的正则表达式： $r_1r_2^*r_3 \cup r_4$ 。我们可以将它分成两部分来解读，第一个部分 $r_1r_2^*r_3$ 描述了原来要从 $q_i$ 经过 $q_r$ 最后到达 $q_j$ 的过程。而第二个部分 $r_4$ 则描述了原来不经过 $q_r$ 直接从 $q_i$ 转移至 $q_j$ 的过程。因为我们要同时兼顾两种可能，所以我们需要用 $\cup$ 将它们连接起来。

对于拥有更多状态的 GNFA，我们只需要按照这个方法，考虑移除某个状态之后，箭头上正则表达式的标签的变化即可。

GNFA 的正式定义

在我们给出引理 2的证明之前，让我们先来看看 GNFA 的正式定义。GNFA 的定义其实和 NFA 的定义非常类似，只不过它的状态转移函数稍微特殊一些，它的输出不是状态子集，而是正则表达式：

\delta: (Q \setminus \{q_{accept}\}) \times (Q \setminus \{q_{start}\}) \to R

其中 $R$ 代表的是定义在字母表 $\varSigma$ 之上的正则表达式的集合， $q_{accept}$ 是接受状态， $q_{start}$ 是起始状态。如果说 $\delta(q_i, q_j) = r$ ，那么 $q_i$ 转移到 $q_j$ 的箭头上的标签就是正则表达式 $r$ 。而按照我们最初对 GNFA 的要求，没有接收状态指向其他状态的箭头，也没有其他状态指向起始状态的箭头，因此函数的定义域为： $(Q \setminus \{q_{accept}\}) \times (Q \setminus \{q_{start}\})$

$\setminus$ 符号代表集合的差集(difference)运算³, 某些资料也使用符号 $-$

我们定义GNFA为一个 5 元组 (5-tuple), 写作 $M = (Q, \varSigma, \delta, q_{start}, q_{accept})$ ⁴，其中：

$Q$ 是有限的集合，叫做状态集
$\varSigma$ 是有限的集合，叫做字母表
$\delta: (Q \setminus \{q_{accept}\}) \times (Q \setminus \{q_{start}\}) \to R$ 是状态转移函数
$q_{start} \in Q$ 是起始状态
$q_{accept} \in Q$ 是接受状态，它是 $Q$ 的一个子集

对于上述定义，我们可以这样描述 GNFA 的计算过程：一个 GNFA 如果接受某字符串 $w \in \varSigma^*$ ，那么对于字符串 $w = w_1w_2...w_k, w_i \in \varSigma^*$ 存在一个状态序列 $q_0,q_1,...,q_k$ 满足：

$q_0 = q_{start}$
$q_k = q_{accept}$
对于每个 $i$ 我们都有子字符串 $w_i \in L(R_i)$ , $R_i = \delta(q_{i-1}, q_i)$ ，换句话说， $R_i$ 是从状态 $q_{i-1}$ 到 $q_i$ 箭头上的正则表达式

证明 (Proof)

现在让我们回到引理 2的证明。首先，我们要证明上述移除 GNFA 状态的转换方法所产生的 $k-1$ 个状态的 GNFA 和移除前的 GNFA 是等价的。首先让我们更形式化的描述这个过程：

对于转换函数 $CONVERT(G)$ ⁴:

使 $k \ge 2$ 为 $G$ 的状态数量
如果 $k = 2$ , 那么 $G$ 一定刚好包含一个起始状态和一个结束状态，两个状态上的标签为正则表达式 $R$ ，函数返回 $R$
如果 $k > 2$ ，选择任意状态 $q_r \in Q \setminus \{q_{start}, q_{accept}\}$ ，然后构造新的 GNFA $G'= (Q', \varSigma, \delta', q_{start}, q_{accept})$ ，其中 $Q' = Q \setminus \{q_r\}$
- 对于任意 $q_i \in Q' \setminus \{q_{accept}\}$ 以及任意 $q_j \in Q' \setminus \{q_{start}\}$ 使得 $\delta(q_i, q_j) = (R_1)(R_2)^*(R_3) \cup (R_4)$
- 其中 $R_1 = \delta(q_i, q_r), R_2 = \delta(q_r, q_r), R_3 = \delta(q_r, q_j), R_4 = \delta(q_i, q_j)$
计算 $CONVERT(G)$ 直到函数返回

我们可以观察到，上述 $CONVERT(G)$ 描述了一个递归的过程，而递归的边界条件是 $k = 2$ 。这个递归过程不会永远进行下去，因为每进行一次递归都会减少一个状态，直到 $k = 2$ 然后返回我们需要的正则表达式。

现在让我们证明命题：对于任意 GNFA $G, CONVERT(G)$ 返回的正则表达式等价于 $G$ 。为此，我们需要使用数学归纳法 (Mathematical Induction)进行证明，我们对 GNFA 的状态数量 $k$ 进行归纳证明：

(1) 归纳奠基:

如果 $k = 2$ ，那么 GNFA 只有两个状态 —— 起始状态和接受状态，以及一个状态转移。该状态转移上的正则表达式标签描述了所有能让 $G$ 进入接受状态的字符串。因此该正则表达式等价于 $G$ 。

(2) 归纳递推:

假设该命题对于 $k-1$ 成立，并利用该假设证明该命题对于 $k$ 也成立。首先我们需要展示 $G$ 和 $G'$ 识别同一个语言。假设 $G$ 接受字符串 $w$ , 那么一定存在某个被接受的计算分支并拥有以下状态序列：

q_{start},q_1,q_2,q_3,...,q_{accept}

如果其中的状态不包含被移除的状态 $q_r$ ，那么很明显 $G'$ 也接受 $w$ 。其原因是该计算分支不经过状态 $q_r$ ，因此会作为 $\cup$ 运算的一部分出现在新的正则表达式标签上。

如果其中的状态包括被移除的状态 $q_r$ ，那么 $q_r$ 前后的状态 $q_i$ 和 $q_j$ 的状态转移包含一个修正过的正则表达式并能够接受所有从 $q_i$ 转移到 $q_j$ 的字符串。因此， $G'$ 也必须接受字符串 $w$ 。

相反地，假设 $G'$ 接受字符串 $w$ 。因为 $G'$ 中任意两个状态 $q_i$ 和 $q_j$ 之间的箭头都描述了在 $G$ 中从 $q_i$ 到 $q_j$ 所需的字符串的集合，该计算过程要么经过状态 $q_r$ ，要么不经过状态 $q_r$ 。那么 $G$ 也必须接受字符串 $w$ 。因此 $G$ 和 $G'$ 等价。

归纳假设声明了，当该算法对 $G'$ 自身进行递归调用时，返回的正则表达式等价于 $G'$ , 因为 $G'$ 此时拥有 $k-1$ 个状态。因此，该正则表达式也等价于 $G$ ，从而证明了该算法的正确性。

最后，通过该证明我们便完成了对 引理 2 以及前文定理的证明（两个方向均已完成证明）。

具体的例子

让我们继续之前的例子，之前我们只是将 DFA 初步转换成了 GNFA (见上文中的步骤 (3))：

现在就让我们将它接着转换为只包含两个状态的 GNFA，假设我们先移除状态 $1$ 。

那么首先我们需要修正状态 $0$ 到状态 $3$ 的状态转移，其正则表达式标签将会变成 $\epsilon 1^* \empty \cup \empty$ 。而上文中提到过，拼接 $\empty$ 仍会得到 $\empty$ ，因此整个正则表达式可以直接简化为 $\empty$ 。

其次，我们还需要修正状态 $0$ 到状态 $2$ 的状态转移（因为它原本也有经过 $1$ 的可能），其正则表达式标签将会变成 $\epsilon 1^* 0 \cup \empty$ ，我们可以将其简化为 $1^* 0$ 。

然后，我们需要修正状态 $2$ 到状态 $2$ 自身的状态转移（因为它原本也有经过 $1$ 的可能），其正则表达式标签将会变成 $(0 \cup 1) 1^* 0 \cup \empty$ ，我们可以将其简化为 $\varSigma 1^* 0$ 。

最后，我们需要修正状态 $2$ 到接受状态 $3$ 的状态转移（因为它原本也有经过 $1$ 的可能），其正则表达式标签将会变成 $(0 \cup 1) 1^* \empty \cup \epsilon$ ，我们可以将其简化为 $\epsilon$ 。

最终我们将得到一个 $k = 3$ 的 GNFA，如下图所示:

紧接着，我们还需要再移除一个状态，这样整个 GNFA 就会只剩下两个状态，从而得到我们想要的正则表达式。在这个例子中，我们现在只能选择移除状态 $2$ ，因为它是除了起始状态和接受状态外唯一的一个状态。修正状态转移之后我们则会得到正则表达式标签： $1^*0(\varSigma 1^* 0)^* \epsilon \cup \empty$ ，我们可以将其简化为 $1^*0(\varSigma 1^* 0)^*$ 。如下图所示:

这样我们就完成了从 DFA 到正则表达式的转换，最终的正则表达式则是唯一的状态转移箭头上的正则表达式标签： $r = 1^*0(\varSigma 1^* 0)^*$ 。

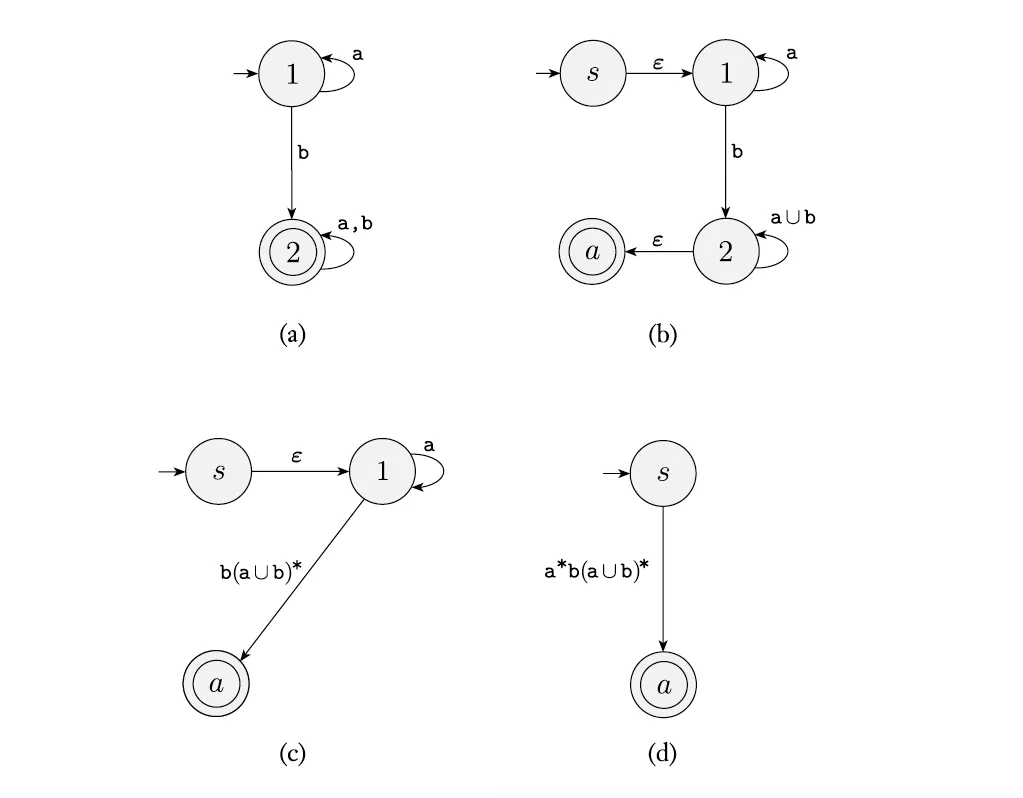
在 DFA 转换到 GNFA 时候，我们通常可以省略 $\empty$ 状态转移，因为最终在消除状态时，这些 $\empty$ 正则表达式标签都会通过 $\cup$ 运算从而被消除掉，如下图中的例子:

总结

本篇文章首先引入了正则表达式及其正式定义，并给出了若干个具体的例子。然后提出了有限自动机和正则表达式的等价性定理，并对其进行了证明。期间，文章引入了 GNFA 这一类有限自动机并着重介绍了 DFA 转换到 GNFA 以及 GNFA 转换到正则表达式的方法。

最后，文章还给出了一些实际的 DFA 转换正则表达式的例子。

后续文章预告

本系列的理论部分到此就基本结束了，下一篇文章将会展示，如何利用这些理论并编写代码实现正则表达式的解析和文本匹配，从而完成本系列文章从理论到实践的闭环。

其他参考资料

Sipser, M., 2012. Introduction to the theory of computation. 3rd ed. Cengage Learning, p.70, Figure 1.61.↩
Sipser, M., 2012. Introduction to the theory of computation. 3rd ed. Cengage Learning, p.71, Figure 1.62.↩
https://proofwiki.org/wiki/Definition:Set_Difference ↩
Sipser, M., 2012. Introduction to the theory of computation. 3rd ed. Cengage Learning, p.73↩