Regular Expression 从理论到实现 - III

前言

本篇文章是 Regular Expression 从理论到实践系列的第三篇文章。

在这个系列里，我将尝试从理论出发，阐述 Regular expression 作为软件开发人员不可或缺的工具背后所蕴含的计算机科学的重要理论，以及如何将这些理论付诸实践（用代码实现）。

或许对大多数开发者来说，掌握一门称手的工具更为重要。但是我希望读者们读完本系列文章之后，也能意识到理论的重要之处。

如果你还没有阅读本系列的第一篇文章，请先移步至：Regular Expression 从理论到实践系列 - I 以及 Regular Expression 从理论到实践系列 - II，否则你将无法很好地吸收和理解本篇文章。

回顾

上篇文章首先介绍了定义在语言上的三个基本运算：

• 并运算 (Union)
• 拼接运算 (Concatenation)
• 闭包运算 (Kleene star/Kleene closure)

然后给出了三个定理，来体现这些运算在正则语言上的封闭性。对于第一个定理，我们介绍了一个简单的证明思路，并举例对其说明。对于后两个定理，因为需要借助新的工具来证明，文章引入了非确定性 (nondeterminism) 的概念。文章最后还给出了 NFA 及其计算的正式定义，并提供了大量的例子以及和 DFA 的对比。

NFA 和 DFA 的等价性 (Equivalence)

上篇文章的结尾留给了读者一个思考问题：

NFA 的计算能力是否比 DFA 更强？或者说是否存在某些问题，通过 NFA 可以解决，而通过 DFA 则不能解决呢？

这个问题的结论是 —— NFA 和 DFA 是等价的，它们都能够识别同一类的语言。

这个结论或许会让某些读者感到惊讶，因为 NFA 直觉上看似比 DFA 更加强大和灵活。通常来说，用 NFA 来描述一个语言比用 DFA 更加简洁直白，这一点也在上篇文章的例子中得到了充分的体现。

我们称两个有限自动机是等价的 (equivalent) 意味着它们识别 (recognize) 的是同一个语言 (language)。

定理 - 每一个非确定有限自动机 (nondeterministic finite automaton) 都有一个对应的等价的确定有限自动机 (deterministic finite automaton)

如果说一个语言能被某个 NFA 识别，我们也必须能够找到一个等价的 DFA，并且这个DFA 能够识别同一个语言。那么我们要如何才能找到这样一个等价的 DFA 呢？

证明思路 (Proof idea)

简单来说，我们可以将 NFA 以某种方式来转化为 DFA 并且用它来模拟原来 NFA 的计算。那么我们如何来用 DFA 模拟 NFA 呢？

在 NFA 的计算模型中，我们需要追踪不同分支的计算情况，根据下一个输入字符，我们需要决定 NFA 接下来的走向（比如是否产生分支）。而我们需要追踪的内容，则是 NFA 的状态。

还记得 NFA 的状态转移函数输出的不是单个的状态，而是可能产生的状态子集吗？假设 NFA 有 $k$ 个状态，那么则有 $2^k$ 个可能的状态子集（见上篇文章的内容)。

对于 DFA 来说，模拟 NFA 的计算就是要记住 NFA 每一个可能产生的状态子集，因此 DFA 需要 $2^k$ 个状态。而 DFA 的起始状态则只需要将原本的起始状态 $q_0$ 变为一个包含它的子集 $\{q_0\}$。

而 DFA 的状态转移函数，则需要接受一个状态子集和一个输入字符作为参数，然后输出一个新的状态子集。

既然 DFA 需要记住 NFA 可能产生的下一个状态子集，那么我们只需要将当前的 DFA 状态 (这个状态本身是一个状态子集) 里面的每一个子状态在 NFA 中接受某个字符时所产生的下一个可能状态集通过并运算合并成一个新的子集，这个新的子集就是 DFA 针对某个输入字符的下一个状态。

假设当前状态是 $\{ a, b \}$, 我们观察输入字符 $1$: 假设在原 NFA 中状态 $a$ 通过输入字符 $1$ 只能转移到状态 $a$, 而状态 $b$ 通过输入字符 $1$ 可以转移到状态 $a$ 和状态 $c$。那么我们则需要 DFA 处于状态 $\{ a, b \}$ 并读取输入字符 $1$ 时转移至状态 $\{ a, b, c \}$

这个过程我们需要对 DFA 中的每个状态对字母表中的每一个字符都进行对应的处理，并确定下一个状态。重复这个过程，我们最终就能得到 DFA 的状态转移函数。

这个证明也是构造性证明 (constructive proof)，该构造也称为幂集构造(power set construction)¹。本篇文章将不提供改构造的形式化的数学表达，感兴趣的读者可以参考引用, 或者参考该 Youtube 视频。

接下来，让我们通过一个具体的例子来理解这个构造。

这个 NFA 是上篇文章中的 $N_4 = (Q, \{a, b\}, \delta, q_1, \{q_1\})$。为了构造一个与 $N_4$ 等价的 DFA, 让我们称其为 $D_4 = (Q', \varSigma, \delta', q_0', F')$。我们需要首先确定 $D_4$ 的状态集 $Q'$：

因为 $N_4$ 有三个状态: $Q = \{q_1, q_2, q_3\}$，因此它一共有 $2^3 = 8$ 个子集，如上式所述。$D_4$ 的字母表和 $N_4$ 一样保持不变，仍旧是 $\varSigma = \{a, b\}$。

接下来让我们确定起始状态和接受状态, 为了方便表达，让我们定义一个辅助函数

那么 DFA 的起始状态 $q_0'$ 可以表达为 $E(\{q_1\})$，也就是可以从原 NFA 的起始状态 $q_1$ 出发，经过 0 次或者多次 $\epsilon$ 转移之后所能够到达的状态的集合。仔细观察上图，不难得出 $E(\{q_1\}) = \{q_1, q_3\} = q_0'$

而 DFA 的接受状态 $F'$，则是任意包含原 NFA 接受状态 $q_1$ 的子集:

接下来我们可以用类似的方法来确定 $D_4$ 的状态转移函数 $\delta'$。在这个例子中，我们的字母表只包含两个字符 $a, b$，因此 $D_4$ 的每个状态都需要对字符 $a$ 和字符 $b$ 定义对应的状态转移。让我们通过几个具体的例子来理解这个过程：

如果我们仔细观察 $N_4$, 状态 $q_1$ 无法读取 $a$ 字符，而状态 $q_3$ 读取一个 $a$ 字符则进入状态 $q_1$ 以及马上通过 $\epsilon$-转移进入 $q_3$, 那么对于 $D_4$ 的起始状态 $\{q_1, q_3\}$，读取 $a$ 字符则会进入状态 $\{q_1, q_3\}$，也可以写作:

而对于 $D_4$ 的起始状态 $\{q_1, q_3\}$，读取 $b$ 字符则会进入状态 $\{q_2\}$, 因为在 $N_4$ 中，从状态 $q_1$ 或者 $q_3$ 开始能读取字符 $b$ 只能进入状态 $q_2$，写作：

类似地:

• 状态 $\{q_1\}$ 读取字符 $a$ 进入 $\empty$, 读取字符 $b$ 进入 $\{q_2\}$
• 状态 $\{q_3\}$ 读取字符 $a$ 进入 $\{q_1, q_3\}$, 读取字符 $b$ 进入 $\empty$
• 状态 $\{q_1, q_2\}$ 读取字符 $a$ 进入 $\{q_2, q_3\}$, 读取字符 $b$ 进入 $\{q_2, q_3\}$
• 以此类推 …

注意：我们这里只允许读取某个字符之后再接着进行 $\epsilon$-转移，不能在读取字符之前就进行 $\epsilon$-转移

如果我们仔细地将 $D_4$ 的状态转移函数确定下来，就会得到如下图的有限状态机：

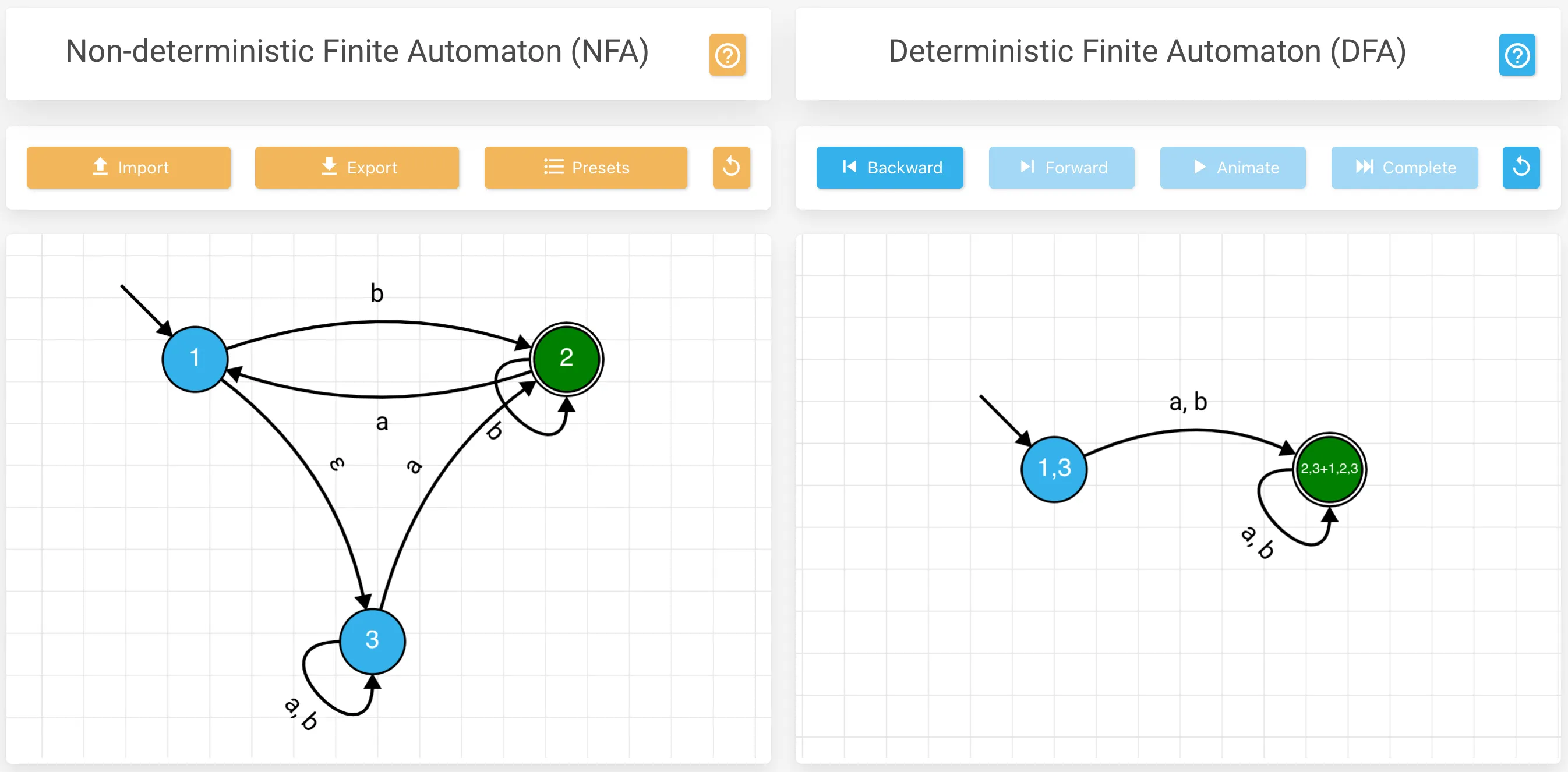
我们还可以简化这个转换后的 DFA，因为仔细观察可以发现，没有任何指向状态 $\{q_1\}$ 和 $\{q_1, q_2\}$ 的箭头，因此我们可以移除这两个状态而不影响该自动机的计算。移除这两个状态后我们得到以下有限自动机：

感兴趣的读者也可以通过 NFA to DFA 在线转换页面 利用该文件导入上述例子中的 NFA，然后观察转换的过程。或者自己创建任意的 NFA，然后观察转换过程：

推论 - 当且仅当存在某一 NFA 能够识别一个语言时，这个语言才是正则 (regular) 的

回顾第一篇文章的内容: 一个语言被称为正则语言 (regular language)，当存在某个能识别该语言的 DFA。

这个推论之后我们还会再用到并回顾，现在我们只需要了解一下该推论。

在这个推论里，我们要注意它的条件 当且仅当(if and if only) —— 也就是说 “某个语言是正则的” 和 “存在某个可以识别这个语言的 NFA” 是等价的，不管从命题的哪个方向，都可以推导出另外一个命题。

通过上文中的定理我们知道，任意 NFA 可以转换成 DFA，这就导致了如果一个 NFA 可以识别某个语言，那么某个 DFA 也可以，所以这个语言是 正则 (regular) 的。

而如果某个语言是正则的，那么根据这个推论，必须存在某个 NFA 并能够识别该语言。这个条件明显也是正确的，因为根据正则语言的定义，我们知道一定存在某个能够识别它的 DFA，而 DFA 本身同时也是一个 NFA。

正则语言的运算的封闭性 (续)

在本系列的第二篇文章中我们简单地探讨了定义在正则语言上的运算的封闭性。在我们引入了 NFA 以及了解了它和 DFA 之间的等价性之后，让我们重新回顾这些性质，并且针对第二篇文章中提出的三个定理给出更易于理解和方便的证明思路。

通过运用非确定性 (nondeterminism) 我们可以让证明变得更加高效和简单。

定理 1: 正则语言的并运算是封闭运算 (续)

首先让我们再回顾一下并运算 (union) 的封闭性。在上一篇文章中，我们通过利用一个 DFA 同时模拟两个 DFA 来证明这条定理。

现在我们要利用非确定性 (nondeterminism) 这个工具来重新证明这个定理。

假设我们有两个正则语言 $A_1$ 和 $A_2$ 并且想要证明 $A_1 \cup A_2$ 也是正则语言。那么我们可以简单地利用两个 NFA, 一个识别 $A_1$，另外一个识别 $A_2$，然后通过 $\epsilon$-转移将这两个 NFA 连接起来，为此我们需要一个新的初始状态。该思路如下图所示：

²

通过这种连接方式，我们便构造出了一个新的 NFA $N$, 它能够识别 $A_1 \cup A_2$。

定理 2: 正则语言的拼接运算是封闭运算 (续)

接着让我们再来回顾拼接运算 (union) 的封闭性。上一篇文章指出了利用 DFA 证明的困难之处 - 新构建的 DFA 没有办法知道两个字符串拼接的确切位置在哪。这个问题我们可以利用 NFA 来轻松解决。

假设我们有两个正则语言 $A_1$ 和 $A_2$ 并且想要证明 $A_1 \circ A_2$ 也是正则语言。那么我们可以简单地利用两个 NFA, 一个识别 $A_1$，另外一个识别 $A_2$，然后通过若干个 $\epsilon$-转移将 $A_1$ 原先所有的接收状态和 $A_2$ 原来的起始状态连接起来。

因为 $A_1$ 在前，所以新的 NFA 只需要采取 $A_1$ 的起始状态作为新的起始状态即可。同理，因为 $A_2$ 在后，所以新的 NFA 只需要采取 $A_2$ 的接受状态作为新的接受状态。该思路如下图所示：

³

通过这种连接方式，我们便构造出了一个新的 NFA $N$, 它能够识别 $A_1 \circ A_2$。

定理 3: 正则语言的闭包运算是封闭运算 (续)

最后让我们再来回顾闭包运算 (closure) 的封闭性。上一篇文章同样指出了利用 DFA 证明的困难之处 - 因为闭包运算本质上利用的是拼接运算。这个问题我们也可以利用 NFA 来轻松解决。

假设我们有一个正则语言 $A_1$ 并且想要证明 $A_1^*$ 也是正则语言。那么我们可以修改能够识别 $A_1$ 的 NFA 然后让它也能够识别 $A_1^*$。具体的操作方法是：

1. 加入一个新的起始状态并将其同时设置为接受状态，然后为其设置一个 $\epsilon$-转移指向原本的起始状态。
2. 为原本所有的接受状态添加一个 $\epsilon$-转移指向原本的起始状态。

第一点解决了 $\epsilon$ 空串本身存在于 $A_1^*$ 当中的问题，第二点解决所有在原 $A_1$ 中可能的字符串进行自身拼接操作的问题。该思路如下图所示：

⁴

通过这种连接方式，我们便构造出了一个新的 NFA $N$, 它能够识别 $A_1^*$。

总结

本篇文章首先展示了 NFA 和 DFA 的等价性 (equivalence)，并提供了一个证明思路，然后引入了一个关于 NFA 和正则语言的重要的推论。接着文章利用 NFA 对上篇文章中提到的三个定理重新提供了新的证明思路。

后续文章预告

本系列的下一篇文章将会介绍正则表达式 (regular expression) 以及它和 NFA/DFA 之间的关联。同时文章还会引入一种特殊的自动机，利用它我们将了解到如何将 NFA/DFA 转化为正则表达式。