Regular Expression 从理论到实现 - II

前言

本篇文章是 Regular Expression 从理论到实践系列 的第二篇文章。

在这个系列里，我将尝试从理论出发，阐述 Regular expression 作为软件开发人员不可或缺的工具背后所蕴含的计算机科学的重要理论，以及如何将这些理论付诸实践（用代码实现）。

或许对大多数开发者来说，掌握一门称手的工具更为重要。但是我希望读者们读完本系列文章之后，也能意识到理论的重要之处。

如果你还没有阅读本系列的第一篇文章，请先移步至：Regular Expression 从理论到实践系列 - I，否则你将无法很好地吸收和理解本篇文章。

回顾

上篇文章介绍了计算理论主要的三个分支，然后简单地介绍了字符串，字母表和语言以及他们的关系，紧接着给出了有限状态机 (finite automaton) 以及基于它的计算模型 (computational model) 的正式定义并列举了不少详细的例子，文章最后引入了正则语言。

在这篇文章中，让我们来探讨和研究一下定义在语言 (regular language) 上的运算，以及这些运算的性质。

正则运算（The Regular Operations）

在算数计算中，基本对象是数字，而定义在数字上的运算符，如 $+, -, *, /$ 都是我们用来操作数字的工具。在计算理论中，这个基本对象则变成了语言(language)，而定义在语言上的运算则让我们可以像对数字进行运算那样来对语言进行运算。

这些定义在语言上的运算，我们称之为正则运算（The Regular Operations）。我们可以通过利用这些运算来研究正则语言的性质。在开始介绍之前，我们需要了解并注意以下几点：

• 语言可以是正则 (regular)，也可以是非正则 (nonregular) 的
• 虽然这些运算被称为正则运算（The Regular Operations），但实际上它们也可以运用在非正则语言上 (因此我们可以统称为语言的运算)
• 后续的文章还会再简短地介绍非正则 (nonregular) 语言（虽然稍微超出了本系列要讨论的范围）

假设 $A$ 和 $B$ 分别为任意两个语言，我们定义以下三个运算：

• 并运算 (Union): $A \cup B = \{ w \mid w \in A \text{ 或者 } w \in B\}$
• 拼接运算 (Concatenation): $A \circ B = \{ xy \mid x \in A \text{ 并且 } y \in B\}$
• 闭包运算 (Kleene star/Kleene closure): $A^* = \{ x_1x_2x_3..x_k \mid k \ge 0 \text{ 并且每个 } x_i \in A \}$

对于大部分读者来说，并运算可能是最好理解的一个运算。它仅仅是将两个语言中的字符串合并在一起从而形成一个新的语言。

拼接运算稍微有一些棘手，它会从语言 $A$ 中提取一个字符串，作为新的字符串的开头，然后再从语言 $B$ 中提取一个字符串，拼接在其后，共同形成一个新的字符串。拼接运算会根据所有可能的组合 — 也就是语言 $A$ 所有的字符串和语言 $B$ 所有的字符串按照上述规则进行拼接的所有可能的组合，形成新的语言。

不同于上面两个运算，闭包运算 (也可以称之为 $*$ 运算) 只需要一个语言来进行运算，也就是说它是一个一元运算 (unary operation)。闭包运算会从被操作语言（比如 $A$） 中提取任意数量的字符串然后拼接在一起，并将所有可能的组合打包形成一个新的语言。

任意数量也包括 0, 因此空串 $\epsilon$ 也属于 $A^*$，无论 $A$ 是什么语言。

觉得有点抽象？没关系，接下来让我们来看一些具体的例子：

使字母表 $\varSigma$ 为 26 个英文小写字母的集合 $\varSigma = \{a,b,c,..,z\}$, 假设 $A = \{hello, hi\}$, $B = \{world, you\}$，那么则有以下运算结果：

• $A \cup B = \{hello, hi, world, you\}$
• $A \circ B = \{helloworld, helloyou,hiworld, hiyou\}$
• $A^* = \{\epsilon, hello, hi, hellohello, hellohi, hihello, hihi, hellohellohello, hellohellohi, ...\}$

对自然数（包含 $0$ 的情况） $\N^0 = \{0, 1, 2, 3, ...\}$ 而言，加法 $+$ 运算是封闭运算 (closed under …)，意思是对于集合 $\N^0$ 中任意的的 $x$ 和 $y$，它们的和 $x+y$ 也属于集合 $\N^0$。相反，除法 $/$ 不是封闭运算，因为，例如 $1 / 2$ 的运算结果不属于 $\N^0$。

总之，如果称定义在某集合上的某某运算是封闭运算，那么该运算的结果也属于该集合。接下来我们将看到：上文提到的三个正则运算都是封闭运算。

定理 1: 正则语言的并运算是封闭运算 (Theorem: The class of regular languages is closed under the union operation)

恭喜你遇到了本系列文章中即将介绍的第一个定理，注意：该定理只适用与正则语言 (regular language)。

让我们稍微重新组织下语言，这个定理还可以这样表述：

证明思路 (Proof idea)

这里只给出大致的证明思路，本定理具体的形式化证明可以参考补充材料: Youtube 视频，课件 1, 课件 2, 或者经典教科书 Introduction to the theory of computation¹。

假设有正则语言: $A$ 和 $B$。因为 $A$ 和 $B$ 是正则语言，根据第一篇文章中最后的正则语言的定义可以得知，一定存在识别语言 $A$ 的某有限自动机 $M_A$和识别语言 $B$ 的某有限自动机 $M_B$。

为了证明 $A \cup B$ 也是正则语言，我们可以利用有限自动机 $M_A$ 和 $M_B$ 来构造一个新的有限自动机 $M$，让这个自动机能够识别 $A \cup B$。

这种类型的证明也被称之为构造类证明 (constructive proof)。

那么我们要如何构造有限自动机 $M$ 呢？当输入字符串能被 $M_A$ 或者 $M_B$ 接受时，$M$ 也必须接受这个字符串。因为 $M$ 需要接受 $A \cup B$ 中的所有字符串。

我们可以用 $M$ 来模拟 $M_A$ 和 $M_B$，当其中一个有限自动机接受该字符串时，$M$ 也接受该字符串，否则拒绝该字符串。

方法 1

我们能否先模拟 $M_A$ 来检查输入字符串，然后再模拟 $M_B$ 来检查输入字符串呢？ —— 答案是不行。还记得有限自动机的计算方式吗 —— 一次读取一个字符，然后进入下一个状态。

如果我们采取这种方式，那么当 $M$ 模拟完 $M_A$ 的时候，$M$ 已经读完了所有的字符串，而有限自动机是没有所谓的 “倒带” 功能的，$M$ 也没法再重新回到字符串的开头，因此我们需要另辟蹊径。

方法 2

既然有限自动机没有所谓的 “倒带” 功能，那么 $M$ 能不能同时模拟 $M_A$ 和 $M_B$ 呢？这样 $M$ 就只需要从头到尾地读取整个字符一次。但是 $M$ 如何才能利用 有限的状态 来同时记录对两个自动机的模拟呢？—— 只需要让有限自动机 $M$ 在一个状态中同时保存 $M_A$ 和 $M_B$ 的状态。因此 $M$ 的每个状态都是一个状态对 (a pair of states)。

假设 $M_A$ 有 $k_1$ 个状态，$M_B$ 有 $k_2$ 个状态，那么所有可能的状态对则有 $k_1 \times k_2$ 个。$M$ 的状态转移 则是从一个状态对到另外一个状态对，这样每读取一个字符，进入到下一个状态对相当于同时更新 $M_A$ 和$M_B$ 这两个有限自动机的状态。

那么，$M$ 的接受状态就是那些包含了 $M_A$ 或者 $M_B$ 的接受状态的状态对。

具体例子

说了这么多，让我们来通过一个具体的例子来更好地理解这个过程。假设我们有以下有限状态机 $M_A$ 和 $M_B$:

$M_A$ 接受所有以 $0$ 结尾的字符串，$M_B$ 接受所有以 $1$ 结尾的字符串。(两个有限自动机都接受空串 $\epsilon$)

根据上图给出的有限自动机，我们现在来构造新的有限自动机 $M$，我们首先需要确定 $M$ 的所有状态 (一共 $2 \times 2$ 个)：

然后需要确定 $M$ 的接受状态 (包含 $M_A$ 或者 $M_B$ 的接收状态的状态对):

然后需要确定 $M$ 的起始状态 (包含 $M_A$ 并且 $M_B$ 的起始状态的状态对，因为 $M$ 要从头开始同时模拟两个自动机):

不难看出，因为 $M_A$ 接受所有以 $0$ 结尾的字符串，$M_B$ 接受所有以 $1$ 结尾的字符串，而他们又都接受空串 $\epsilon$，那么 $M$ 应该接受所有的由 $0$ 或者 $1$ 组成的字符串。

接下来我们根据 $M_A$ 和 $M_B$ 的状态转移以及 $M$ 的状态集，来确定 $M$ 的状态转移，$M$ 每次读取一个字符，都会根据 $M_A$ 和 $M_B$ 预设的状态转移，来同时更新状态对中的状态，然后进入到下一个状态对:

这样我们就构造出了到了有限状态机 $M$, 而 $M$ 能够同时识别 $M_A$ 所能识别的语言，以及 $M_B$ 所能识别的语言，因此：$M$ 能够识别语言 $A \cup B$，写作 $L(M) = A \cup B = L(M_A) \cup L(M_B)$

注意：在上述例子中，我们把 $M_B$ 的状态放在了 $M$ 的状态对的第一位（括号里的第一位），反过来也是成立的，我们只需要稍微调整一下状态的顺序和状态转移即可。

定理 2: 正则语言的拼接运算是封闭运算 (Theorem: The class of regular languages is closed under the concatenation operation)

同定理 1，这个定理也只适用于正则语言 (regular language)。

让我们稍微重新组织下语言，这个定理还可以这样表述：

要证明这个定理，我们可以像证明上一个定理一样，尝试构造一个新的有限自动机来模拟已有的两个自动机 $M_A$ 和 $M_B$。但是对于拼接运算，我们必须在模拟中想办法将输入字符串拆成两份，前者需要被 $M_A$ 接受，而后者需要被 $M_B$ 接受。

但这种方法带来了一个问题：新构建的有限自动机 $M$ 没有办法知道两个字符串拼接的确切位置在哪，比如说我们将字符串 $hello$ 和字符串 $world$ 进行拼接并得到新的字符串 $helloworld$。

这个新的字符串 $helloworld$ 将会作为 $M$ 的输入，而对于 $M$ 而言，这个字符串有可能是 $h$ 和 $elloworld$ 或者是 $hellow$ 和 $orld$ 的拼接 … 那么在没有办法确定确切的拼接位置的情况下，这个办法就行不通了。

为了解决这个问题，我们需要引入一些新的工具 — 非确定性 (nondeterminism)，但在我们研究这个新的工具之前，让我们快速了解一下第三个定理。

定理 3: 正则语言的闭包运算是封闭运算 (Theorem: The class of regular languages is closed under the kleene-star/closure operation)

同定理 1 和定理 2，这个定理也只适用于正则语言 (regular language)。

让我们稍微重新组织下语言，这个定理还可以这样表述：

同定理 2 一样，要证明这个定理的成立，我们也必须借助非确定性 (nondeterminism) 这个概念。接下来就让我们仔细研究一下这个概念。

非确定性 (nondeterminism)

非确定性 (nondeterminism) 在计算理论领域，乃至在整个计算机领域都发挥着非常重要的作用。

在本文的讨论范围之内，之前所提到的有限自动机的计算都是确定的 (deterministic) —— 计算的每一个步骤都是独一无二的，也就是说当我们的自动机处于某个特定的状态时，给定某个特定的字符输入，这个自动机必将进入下一个确定的状态。

这一点在定义自动机的状态转移函数时就牢牢确定下来了，因此，通过观察自动机的图表，我们就能很清楚的地知道接下来会发生的变化。

而对于非确定的 (nondeterministic) 有限自动机来说，在每个计算的步骤中存在多种不同的选择来决定自动机的下一个状态，为了方便起见我们将简称确定有限状态机为 DFA (deterministic finite automaton)，非确定有限状态机为 NFA (nondeterministic finite automaton)。

让我们先来看一个具体的 NFA 的例子:

这个 NFA 接受任何包含子字符串 (substring) $101$ 或者 $10$ 的非空字符串，让我们命名它为 $N_1$。

留给读者思考：如果我们要用 DFA 来接受相同的语言，这个 DFA 应该是什么样的呢？

从上图我们看出，DFA 和 NFA 的区别还是很明显的：

• 首先，DFA 的每个状态对字母表中的每一个字符，都有且只有一个状态转移 (transition)。(如果你不确定的话，可以回到前文再仔细观察一番)
• NFA 的每个状态对字母表中的每一个字符，可以有且任意多个状态转移 (transition) (0 个也是允许的，这一点我们观察上图就可以发现)
• NFA 允许 $\epsilon$ 出现在状态转移上（也就是不需要读取任何字符就可以进入到下一个状态，这一点我们可以观察上图 $q_{10}$ 和 $q_{101}$ 之间的状态转移可以得知）

注意：文中给出的 NFA 也叫做 $\epsilon$-NFA，也就是允许 $\epsilon$-状态转移的 NFA (NFA with $\epsilon$-moves)，$\epsilon$-NFA 是普通 NFA 更加通用的形式²。

对于本文而言，使用 $\epsilon$-NFA 可以更加简化我们的举例和对某些应用的表达，如果读者在其他材料中看到普通的 NFA 也不要担心，任意的 $\epsilon$-NFA 都可以消除 (eliminate) $\epsilon$-状态转移并转换为一个等价的普通 NFA。 感兴趣的读者可以阅读这个课件，或者这个页面

NFA 的计算过程

NFA 看起来要比 DFA 简洁很多，那么在每个状态都可能有多个可选择的状态转移的情况下，要如何来表达 NFA 的计算过程呢？

假设我们正在运行一个 NFA，并且提供了某个输入字符串。假设 NFA 当前处于某个状态，并且到下一个状态有多种不同的状态迁移可选。

例如，当前上图的 $N_1$，假设当前状态是 $q_0$，下一个字符是 $1$。在读取下个字符之后，这个 NFA 会产生分支，分别对应读取字符 1 之后发生的不同的状态迁移，并且并行 (parallel) 地对每个分支进行后续的计算，而后续的计算可能会继续产生新的分支。

我们可以这样想象：每当出现一个分支时，NFA 都会产生一个拷贝，然后沿着当前的路径继续进行计算。而每个拷贝之间互相独立，互不影响，并且可以同时进行计算。

假如下一个读取的字符没有任何可用的状态转移，那么当前的这个分支就会停止计算。

总之，如果任意一个计算分支在读取完所有的字符之后最终处于接受状态，那么整个 NFA 就接受 (accept) 这个字符串。

因此非确定性 (nondeterminism) 可以看作是一种并行的计算，其中有多个 “进程（processes）” 或者 “线程 (threads)” 同时进行计算。当 NFA 发生分叉时，可以看做是当前的 “进程（processes）” fork³ 出了一些 子进程 (child processes), 然后这些子进程再分别进行各自的计算。

另外一种看待非确定性 (nondeterminism) 的方式是，把整个计算过程想象成一棵树 (tree)，树的根 (root) 象征着计算的开始，每一棵子树 (subtree) 都代表着在这个节点有多种不同的状态迁移的可以选择，因此计算产生了分叉。当任意一个叶子节点 (leaf) 处于接受状态时，整个 NFA 则接受当前字符串。

下面这张图非常生动形象地展示了这一过程：

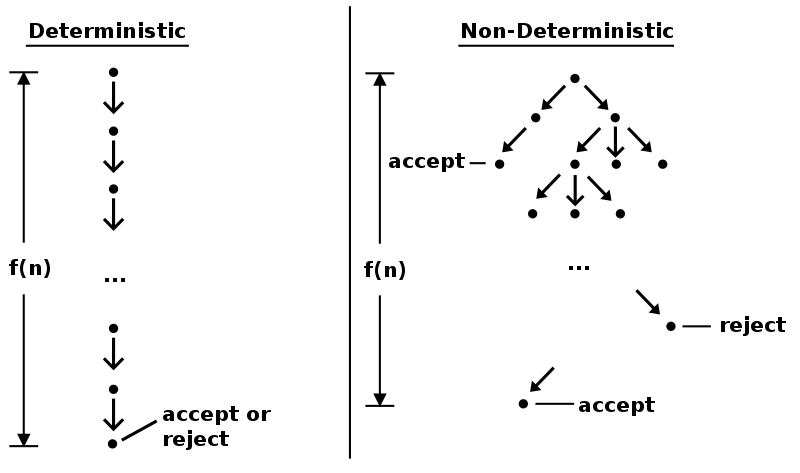
现在让我们看看 NFA $N_1$ 的一个实际的计算例子，假设 $N_1$ 根据输入字符串 $01010$ 进行计算:

我们可以发现每当 NFA $N_1$ 处于状态 $q_0$ 并读取字符 $1$ 时，计算路径就会产生分支，对应我们在 $N_1$ 的状态图中所看到的状态转移（存在两种可能）。

其中值得注意的是，当 NFA $N_1$ 处于状态 $q_1$ 并读取字符 $0$ 时，因为存在 $\epsilon$-状态转移的可能，所以计算路径也会产生分支，也就是说同时存在以下两种可能:

1. $\delta(q_1, 0) = q_{10}$ — 不发生 $\epsilon$-状态转移
2. $\delta(q_1, 0) = q_{10} \to \delta(q_{10}, \epsilon) = q_{101}$ — 立即发生 $\epsilon$-状态转移

在 NFA 最后产生的所有分支里，我们可以看到中间和最右边的这个分支（箭头标记加粗）最后处于接受状态，那么我们便可以确定：NFA 最后接受字符串 $01010$。

留给读者思考：我们在上图中能够看到 NFA 是允许 $\epsilon$-状态转移的，那么 DFA 是否也允许 $\epsilon$-状态转移？

Examples: 若干个 NFA 具体的例子

接下来让我们再来看看几个具体的 NFA 以及他们对应的 DFA:

例子 I

以下 NFA $N_2$ 接受字母表 $\varSigma = \{0, 1\}$ 上的任意倒数第二个字符为 $1$ 的字符串：

与之等价的 DFA $D_2$ 为:

留个读者思考：你能看出上图 DFA 中的规律吗？请尝试用自己的语言描述上图 DFA 和 NFA 的计算过程。

例子 II

以下 NFA $N_3$ 接受字母表 $\varSigma = \{0\}$ 上（这类只包含一个字符的字母表也称为一元字母表 (unary alphabet)）的形为 $0^k$ 的字符串，其中 $k$ 只能为 $2$ 或者 $3$ 的倍数：

与之等价的 DFA $D_3$ 为:

留个读者思考：你能看出上图 DFA 计算的规律吗？请尝试用自己的语言描述一下这上述 DFA 和 NFA 的计算过程。

我们可以从上面的例子看出，NFA 相对 DFA 而言，更加容易构造。因为它需要的状态和状态转移的数量比 DFA 更少，表达计算也更加直白并且容易理解。

例子 III

这里我们再给出一个简单的 NFA $N_4$，请读者自行用它来模拟针对一些字符串的计算过程，比如: $\epsilon$, $a$, $baba$, $baa$, $b$, $bb$, $babba$ 等字符串，看看该 NFA 接受和拒绝哪些字符串。

下一篇文章我们会以这个 NFA 为例来展示如何将一个 NFA 转换成 DFA。

非确定有限自动机的正式定义 (Formal Definition of A Nondeterministic Finite Automaton)

按照惯例，再给出了大量的例子之后，让我们一起来看看 NFA 的正式定义：

我们定义NFA为一个 5 元组 (5-tuple), 写作 $M = (Q, \varSigma, \delta, q_0, F)$⁴，其中：

• $Q$ 是有限的集合，叫做状态集
• $\varSigma$ 是有限的集合，叫做字母表
• $\delta: Q \times (\varSigma \cup \{ \epsilon \}) \to \mathcal{P}(Q)$ 是状态转移函数 (读作 delta)
• $q_0 \in Q$ 是开始状态
• $F \subseteq Q$ 是有限的接受状态的集合，它是 $Q$ 的一个子集

NFA 的正式定义和 DFA 的正式定义非常地相似，他们都有字母表，状态集，状态转移函数，开始状态以及接受状态集。但是他们有一些明显的区别：

DFA 的状态转移函数 $\delta$ 接受一个状态和一个字符作为输入，然后输出下一个状态，而 NFA 的状态转移函数 $\delta$ 接受一个状态和一个字符或者 $\epsilon$ 然后输出下一个所有可能的状态的集合。

为了表达 所有可能的状态的集合，我们需要借助新的符号 $\mathcal{P}(Q)$ 来表示 $Q$ 的所有子集。这里的 $\mathcal{P}(Q)$ 也被称为集合 $Q$ 的 幂集 (power set)。

定理⁵: 对于任意集合 $S$, 且 $|S| = n, n \in \N^0$，那么 $S$ 的幂集 $\mathcal{P}(S)$ 一共包含 $2^n$ 个元素，写作 $|\mathcal{P}(S)| = 2^n$。 例如：$S = \{x, y, z\}$，那么 $\mathcal{P}(S) = \{\empty, \{x\}, \{y\}, \{z\}, \{x, y\}, \{x, z\}, \{y, z\}, \{x, y, z\}\}$，其中 $\empty$ 为空集。

上面这个定理我们之后还会再用到。

现在让我们再来仔细观察一下上文中提到的 NFA $N_1$:

根据 NFA 的正式定义，我们可以正式地描述 $N_1$:

$N_1 = (Q, \varSigma, \delta, q_0, F)$, 其中：

• $Q = \{q_0, q_1, q_{10}, q_{101} \}$
• $\varSigma = \{ 0, 1 \}$
• $\delta$ 则可以通过一个表格来描述：

  	$0$	$1$	$\epsilon$
  $q_0$	$\{q_0\}$	$\{q_0, q_1\}$	$\empty$
  $q_1$	$\{q_{10}\}$	$\empty$	$\empty$
  $q_{10}$	$\empty$	$\{q_{101}\}$	$\{q_{101}\}$
  $q_{101}$	$\{q_{101}\}$	$\{q_{101}\}$	$\empty$

• $q_0$ 是起始状态
• $F = \{ q_{101} \}$, 结束状态只有一个

我们可以从表格和图表看出，状态转移函数对 $q_1$ 和输入字符 $1$ 没有确定的输出（图中缺少对应的箭头），那么我们定义它的输出为空集 $\empty$

NFA 计算的正式定义 (Formal Definition of Computation for an NFA)

NFA 的计算的正式定义和 DFA 的非常相似，使 $N = (Q, \varSigma, \delta, q_0, F)$ 为 NFA，$w = w_1w_2...w_n$ 为字母表 $\varSigma$ 上的一个字符串，其中 $w_i \in (\varSigma \cup \{\epsilon\})$。

那么 NFA $N$ 接受 (accept) 字符串 $w$，如果存在一个连续的状态序列 $r_0r_1...r_n$, 其中 $r_i \in Q$ 并满足以下 $3$ 个条件:

1. $r_0 = q_0$
2. 对 $i = 0,1,...,n-1$ 有 $r_{i+1} \in \delta(r_i, w_{i+1})$ 并且
3. $r_n \in F$

条件 1 确保 NFA 必须从起始状态开始计算。条件 2 确保计算过程根据定义好的状态转移 (transition) 从一个状态转移到另外一个可能的的状态，因为 $\delta(r_i, w_{i+1})$ 输出的是一个包含所有可能的状态的集合(这点我们可以通过观察上面的表格得出)。条件 3 确保自动机停止时处于接受状态。

同理，我们说 NFA $N$ 识别 (recognizes) 语言 (language) A，如果 $A = \{ w \mid N \text{ 接受字符串 } w\}$

总结

本篇文章首先介绍了定义在语言上的三个基本运算：

• 并运算 (Union)
• 拼接运算 (Concatenation)
• 以及闭包运算 (Kleene star/Kleene closure)

然后给出了三个定理，来展示这些运算在正则语言上的封闭性。对于第一个定理，我们介绍了一个简单证明的思路，并举例说明。对于后两个定理，需要借助新的工具来证明，接着文章引入了 非确定性 (nondeterminism) 的概念。文章最后给出了 NFA 及其计算的正式定义，并提供了大量的例子以及和 DFA 的对比。

后续文章预告

本系列的下一篇文章将会研究 DFA 和 NFA 之间的关系，然后提供一个将 NFA 转换为 DFA 的通用方法，以及补充后两个语言运算的证明思路。

留给读者思考：在本文中，我们看到了 NFA 的便捷和强大之处，那么 NFA 的计算能力是否比 DFA 更强呢？或者说是否存在某些问题，通过 NFA 可以解决，而通过 DFA 则不能解决呢？